Aljabar
Nama : Annisa Eka Fadhilah
NIM : 2001105020
Kelas : 2D
Materi Kelas 7 SMP Semester 1 Bab 3
Bentuk Aljabar, Rumus Aljabar, dan Operasi Aljabar
Blog ini penulis dedikasikan untuk semua orang yang peduli terhadap pendidikan, khususnya dalam bidang Matematika. Untuk para guru, mahasiswa, siswa, maupun orang tua. Keberadaan blog ini diharapkan dapat membantu guru mencari bahan referensi dalam melakukan pembelajaran di kelas. Baik mengenai model-model pembelajaran yang akan mereka terapkan maupun media pembelajaran yang akan dipakai.
Bagi mahasiswa, blog ini diharapkan mampu menjadi bahan rujukan dalam mencari mata kuliah mereka, informasi umum mengenai perkuliahan, serta dapat menjadi tutorial dalam tugas-tugas kuliah, seperti pengetikan, pembuatan presentasi dan sebagainya. Sama halnya bagi siswa. Blog ini diharapkan mampu memberikan motivasi lebih kepada mereka untuk terus belajar dan terus berkarya. Untuk para orang tua, blog ini diharapkan mampu menjadi panduan mereka dalam memberikan pendidikan di luar sekolah bagi putra-putri mereka.
Pada blog ini akan lebih ditekankan mengenai aljabar. siapa yang pernah dengar kata aljabar? Ini merupakan satu cabang matematika dalam pemecahan masalah dengan menggunakan huruf-huruf untuk mewakili angka-angka. Berasal dari bahasa Arab, al-jabr yang artinya penyelesaian. Kamu tahu siapa penemunya? Ia merupakan cendikiawan bernama Al-Khawarizmi. aljabar yang akan dibahas pada blog ini, antara lain Pengertian Aljabar, Bentuk Aljabar, Rumus Aljabar, dan Operasi Aljabar.
A. Pengertian Aljabar atau Algebra
Aljabar adalah bagian dari ilmu matematika meliputi teori bilangan, geometri, dan analisis penyelesaiannyaSecara harfiah, aljabar berasal dari bahasa arab yaitu الجبر atau yang dibaca "al-jabr". Ilmu ini dibuat oleh Muḥammad ibn Mūsā al-Khwārizmī dalam bukunya mengenai konsep dan bentuk aljabar ditulis sekitar tahun 820, yang merupakan seorang matematikawan, astronomer, dan geograf. Ia dijuluki sebagai "The Father of Algebra". Dalam bahasa inggris, aljabar dikenal dengan istilah "algebra".
B. Bentuk Aljabar
Bentuk aljabar adalah teknik yang digunakan untuk menyajikan suatu masalah matematika dengan simbol atau huruf sebagai peubah suatu objek dalam masalah tersebut. Terdapat 7 istilah umum yang perlu diketahui untuk memahami bentuk suatu aljabar dasar, yaitu:
1. Rumus Persamaan
Persamaan adalah suatu teknik matematika yang digunakan untuk menyamakan suatu permasalahan ke bentuk matematika dengan tanda persamaan atau sama dengan (=). Bentuk ini dapat berupa bentuk yang paling sederhana hingga kompleks. Persamaan dapat digunakan untuk membentuk suatu rumus matematika terhadap suatu masalah.
Contoh :
Masalah :
Jumlah kelereng Xeon dan Yuni adalah 10 buah. Jika kelereng yuni sebanyak 3 buah. Berapa jumlah kelereng Xeon?
Diketahui :
Ubah kelereng Yuni menjadi variabel y
Ubah kelereng xeon menjadi variabel x
y = 3
x + y = 10
Catatan : x + y = 10 merupakan persamaan matematika dari jumlah kelereng Xeon dan Yuni
Ditanyakan :
berapakah nilai x?
Penyelesaian :
x + y = 10
x = 10 - y
Pada dasarnya untuk memindahkan suatu nilai ke ruas lain, sama artinya dengan menghilangkan nilai tersebut di ruas asal. Berikut penjelasannya untuk kasus diatas.
x + y = 10
x + y - y = 10 - y
x = 10 - y
Sehingga, untuk mempercepat perhitungan dapat langsung menulis lawan nilai yang dipindahkan.
x + y = 10
x = 10 - y
Diketahui nilai y = 3, diperoleh
x = 10 - 3
x = 7
Karena nilai x = 7
Jadi, Kelereng Xeon berjumlah 7 buah
2. Variabel (Peubah)
Variabel adalah suatu simbol atau huruf yang digunakan untuk menggantikan suatu nilai yang bersifat tidak tetap (berubah-ubah tergantung persamaan yang memuatnya). Variabel dalam bahasa inggris dise but dengan "variable" (dieja ˈve(ə)rēəbəl) , dan juga disebut "peubah" dalam bahasa Indonesia. Variabel dapat disimbolkan dengan huruf latin (a, A, b, B, c, D, dan seterusnya).
3x + 4y + z = 0
Pada persamaan tersebut, terdapat 3 variabel, yaitu x, y dan z.
3. Koefisien (Coefficient)
Koefisien adalah nilai yang digunakan untuk mengalikan suatu variabel. Koefisien dalam bahasa inggris disebut dengan "coefficient". Nilai koefisien = 1 dapat tidak ditulis.
3x + 4y + z = 0
- nilai koefisien x adalah 3.
- nilai koefisien y adalah 4.
- nilai koefisien z adalah 1 (Koefisien 1 dapat tidak ditulis).
3.1 Menghitung variabel dengan koefisien
Suatu persamaan 3x = 12, berapakah nilai variabel x ?
Penyelesaian :
3x = 12
3. x = 12
x = 12/3 = 4
Catatan : perpindahan koefisien suatu ruas = membagi ruas lain dengan nilai koefsisien tersebut.
Jdi, variabel x = 4
3.2 Menghitung variabel dengan koefisien pada persamaan
Menghitung nilai koefisien menjadi lebih kompleks saat ia berada pada suatu persamaan
3x + 12y = 6
Untuk menyelesaikan solusi variabel x dapat diperoleh dengan memisahkan semua objek selain x keruas kanan, berikut:
3x + 12y = 6
3x = 6 - 12y
x = 6/3 - 12y/3
x = 2 - 4y
Untuk menyelesaikan solusi variabel y dapat diperoleh dengan memisahkan semua objek selain y keruas kanan, berikut:

4.2 Contoh konstanta pada rumus khusus
Suatu konstanta pada rumus-rumus khusus disimbolkan dengan nilai tertentu, misalnya rumus keliling lingkaran :
Suatu variabel dalam suatu bentuk aljabar dapat memuat pangkat (eksponen). Operasi pangkat mempunyai prioritas kedua sejajar dengan operasi akar setelah tanda kurung dalam operasi hitung matematika.
6. Derajat
Derajat pada suatu bentuk aljabar adalah nilai pangkat tertinggi yang dimuat variabel bentuk aljabar, berikut contohnya:
| Bentuk Aljabar | Derajat |
| 3x | 1 |
| 3x2 + 1 | 2 |
| 3x2 + 2x + 1 | 2 |
| 4x4 + 2y2 + 1 | 4 |
| 5x6 + y | 6 |
7. Suku
| Aljabar | s1 | s2 | s3 | s4 | suku |
| 2x | 2x | - | - | - | 1 |
| 2x+1 | 2x | 1 | - | - | 2 |
| 3x2+2x-1 | 3x2 | 2x | 1 | - | 3 |
| 4x3+3x2+2x-1 | 4x3 | 3x2 | 2x | 1 | 4 |
| dan lainnya | ... | ... | ... | ... | ... |
Suku-suku bentuk aljabar dibedakan menjadi suku sejenis dan suku tak sejenis:
Operasi penjumlahan dan pengurangan aljabar hanya dapat dilakukan pada suku-suku sejenis.
Contoh 1: Menyederhanakan aljabar
Sederhanakan bentuk aljabar 2x + 3y + 7x - 2y?
Penyelesaian:
urutkan suku-suku yang sejenis2x + 3y + 7x - 2y= 2x + 7x + 3y - 2y= (2x + 7x) + (3y - 2y)= 9x + y
Jadi, bentuk sederhana dari 2x + 3y + 7x - 2y adalah 9x + y
C2. Operasi Perkalian Aljabar
Contoh 1: Perkalian dengan konstanta
Perkalian dengan konstanta dilakukan dengan mengalikan nilai koefisien masing-masing variabel yang dioperasikan.
2y × 3 = 6y- (3y + x) × 4= (3y × 4) + (x × 4)= 12y + 4x
3yz × 7 = 21yzy × y = y2- x2 × x= x2 + 1= x3
2yz × y = 2y2z- (2x + 1) y= (2x × y) + (1 × y)= 2xy + y
Contoh 2: Perkalian dengan variabel
perkalian dengan variabel dilakukan secara menyeluruh, baik koefisien maupun variabelnya.
C3. Operasi Pembagian Aljabar
Untuk mempermudah operasi pembagian aljabar, dilakukan dengan cara mengubah ke bentuk pecahan.
Contoh 1: Pembagian variabel dengan konstanta
Contoh 2: Pembagian variabel dengan variabel
Contoh 3: Pembagian variabel dengan variabel yang lebih kompleks
C4. Operasi Perpangkatan Aljabar
Contoh 1:




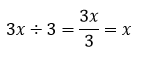
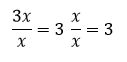
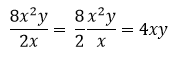
Komentar
Posting Komentar